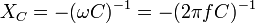16
Other (Public) / Re: Low cost tweezers type LCR meter
« on: November 07, 2011, 10:39:31 AM »
Progress so far:
1. SMD probe
For my tweezers I need some SMD probes.
At first I was planning to buy one, but pricing are too high for my taste.
So I search for alternatives on net and I find this:

Therefore I plan to use only wire in middle and GND all around.
2. Protection from charged capacitors
Almost all measurement tools for capacitors have warning not to connect charged capacitor.
My LCR tweezers have the same problem, so to solve it I decide to place something between probes to shorten them.
Then if I grab charged capacitor with probes, it will be discharged.
To perform measurement I plan using switch to signal device for breaking short point and begin measurement.
With that, tweezers will be protected from discharging current and consume less power, because it will do measuring only when button is pressed.
Big problem is what to use. Obviously choice will be relay, however they are all big.
Smaller ones are reed relays but they can sustain only small currents.
Another problem with relays is that they consume a loot of power during operation.
Using MOSFET is better solution however for this I need at least 10V for gate.
That means adding voltage doublers or more. Another problem is that this protection doesn’t work when device is powered off.
So on end I decide to use switch for shortening/breaking probes and signaling device to begin measurement.
3. Digitally selected wide range of resistors
Now, what I really need is not simple 6 point selector for predefined 6 resistors like in standard DMMs.
Main problem for accurate testing resistors in voltage divider setup is to get proper resistor pair for targeted output voltage.
In measuring capacitance and inductance this isn’t that significant because I can change frequency and match reactance to used resistor.
Ideal digital potentiometer for my need would be one with range from 0 to 10Mohm in resolution of 1 ohm.
Simply put, to achieve this I’ll need 10 million combinations and this can be done with 24 bit – at least 24 resistors + switches to get from 0 to 16777215 ohms in 1 ohm resolution.
This solution of 24 bits is too big and using single chip digital potentiometers have other problems.
Biggest digital potentiometer what I found have 1Mhom (AD5241BRZ1M) in 8bit increment.
That means increment of about 3.9 kohms. But I’ll need 10 of them in series to get 10Mohms.
Fine tuning to increment of 0.39ohms can be done by putting another two of 10kohm and 100 ohm in series, however big issue is frequency bandwidth which is limited to 6 kHz.
So for my purpose digital potentiometers are not good enough.
3.1. Digital selector (shift register, microprocessor?)
So I have to do it with switches and resistors.
When it comes to selecting it is big question how to do it.
Shift register is my first choice but having lot resistors to select means calculations for them how to select it.
Now my microcontroller for this purpose must already calculate guessed value for resistor, then find/calculate closest one available from list which contains calibrated values for each resistor and then set it up.
These calculations require a loot of memory, especially for storing calibrated values.
Another microcontroller can be handy, with extra memory designated to serve only for resistors.
I find out that price between shift registers and microcontrollers are almost identical, so I chose to go with another microcontroller as replacement for shift register.
There are some other advantages in using microcontroller; mainly entire device becomes modular with two separated programming.
Another one is that main microcontroller no longer stores detailed data for each resistor and don’t have to calculate for them.
Basically my idea is; when it calculate guessed resistor, it will send that value to second microcontroller.
That one would find/calculate closest resistance for measure and return that value + set up resistors to that value.
For numerous reasons which I wouldn’t discuss here I decide to go with Microchip PICs microcontrollers.
For my needs I require 16 pins for selecting resistors thru switches (see 3.3. for number) + 3 for SPI serial communication between main microcontroller/PC and this one.
This is total of 19 pins, so suitable PIC with at least 19 I/O and Serial Communication module are PIC16F1516 and PIC24F16KA102 series.
I deicide to go with PIC24 series and main reason is speed – faster calculations, even this series is double the price of PIC16 series.
3.2. Analog switchers or Reed relays?
Now about switches; the best would be to use reed relays but this can take up much of space and most important one: consume significant amount of current in operation.
So I discard them as solution.
Analog switches are worst solution especially if used in series, but there are now available better switches than old CD4066.
I find that FSA2267 with 0.35 ohm on resistance and 45 MHz bandwidth is far better solution.
So I chose to use this switches instead.
3.3. Chosen set of resistors for optimal resistor range
This was tough one and I spend a loot of time on this.
First there was problem of deciding what setup to use; resistors in series or parallel configuration.
There are advantages and disadvantages to both.
Parallel combination provides easier calibration and reduction in errors by division - to some degree.
A problem with this is non linear result due division and calculations for selected resistor must be performed in floating point math, which is problematic with microcontroller.
When using resistors in series like ladder, analog switches are adding up their resistance resulting bigger error and problematic calibration.
On other hand result is linear and easy to calculate/set.
So even I decide at first to go with parallel combination, low resolution vs. number of resistors at higher resistance range was too great to be satisfactory.
At end I decide to go with series setup.
Obviously 24 resistors are too much and 6 are minimum.
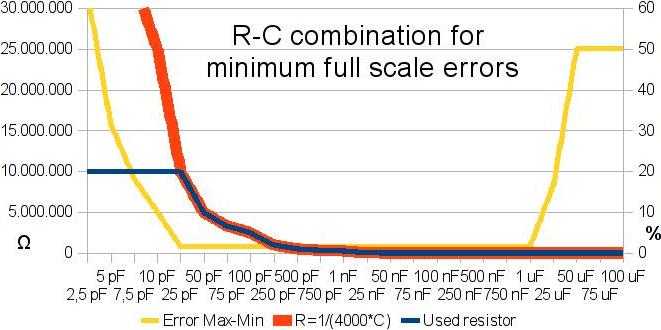
Usually minimal set of resistors to cover entire range would be 200, 800, 9k, 90k, 900M and 9M ohms – 6 bits to cover.
Now the question is why using these exponential values?
What is optimal resolution and accuracy?
To answer these questions, I make this graph:
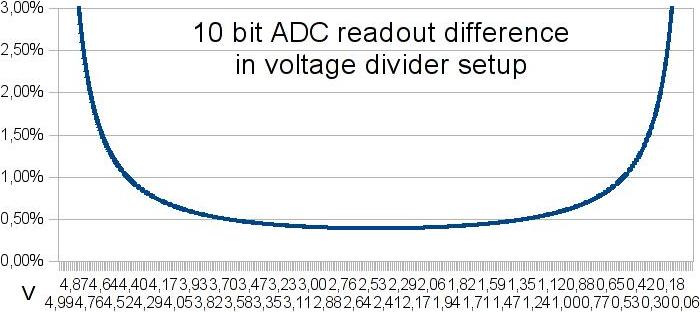
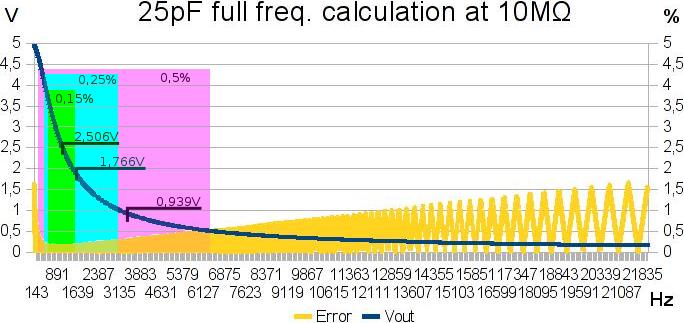
Here is shown difference between two values at different ADC readout points.
10 bit ADC can distinguish about 4.89mV.
So in ideal environment using 1k for testing another 1k resistor, ADC readout will be 2.5024437928V or 2.4975562072V.
After calculation we get 1001.9569471624 or 998.046875 ohms.
In both results, difference or error from real value is 0.1953125%.
As can be seen on graph, this small error is only at mid point.
Going to any edge (bigger resistor difference) produces larger error.
Note that this error is identical for any voltage. So targeting half of input voltage will get the best possible result.
To reduce this error, 12bit ADC will be better solution, which I plan to use.
My soundcard have already 16bit ADC so designing for 12bit ADC will be better solution.
To get best resolution and accuracy is to have only ADC error.
In 10 bit ADC resolution for 100 ohm is 0.1953125 ohm, for 1 kohm 1.953125 ohm up to 10 Mohm and 19531.25 ohm resolution.
Using 10 kohm resolutions at 10 Mohm measuring range is waste, because it doesn’t affect reading at ADC.
However at 12 bit ADC this would have big difference, because minimal resolution for 10 Mohm is 4882.8125 ohms.
So from this math by rounding values of 12 bit ADC, I got these resolutions:
Lowest safe resistor is 200 ohms (16.5mA at 3.3V) and best resolution at 200 ohm is 0.1 ohm (rounded).
Starting from here including possible errors and number of switches I decide to start with resolution of 1 ohm.
In range from 200 ohms to 10 kohms in resolution of 1 ohm, resistor in series must be: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096 and 8192 ohms.
This is 14 bits or 14 switches with these resistors to make that range and it’s obviously already too much.
If best resolution is multiplied by 100, errors in reading will increase by 0.000061% and will not cross 0.2% error of 10 bit ADC, which is acceptable.
For this, new resistor series in range 200 to 1 kohm would be: 10, 20, 40, 80, 160, 320 and 640 ohms with resolution of 10 ohms.
For 1k to 10k range 50 ohm resolution is needed and we use previous resistors to continue into this series: 800, 1600, 3200 and 6400 ohms.
So far 10 bits and to complete series to 10 Mohms another 12 bits are needed which is in total too much.
If resolution was increased by 1000 times, this will increase error by 0.00406% and become 0.101688021% well below 0.2% error.
Series for this resolution will be: 100, 200, 400, 800, 1k, 2k, 4k, 8k, 10k, 20k, 40k, 80k, 100k, 200k, 400k, 800k, 1M, 2M, 4M and 8M ohms.
Total of 20 bits, but this series can be optimized further, if lower resistances are combined together they form enough value to eliminate next bigger resistor.
100+200+400+800=1500 ohms which covers 1k range and with resolution in 1k-10k range of 500 ohms this fits perfectly next in line to 2k. So 1k resistor can be eliminated.
Optimization method will also eliminate others too; 10k, 100k and 1M ohm.
Now, this form series of 16 bits/switches and this is first case below 20bits which I find acceptable.
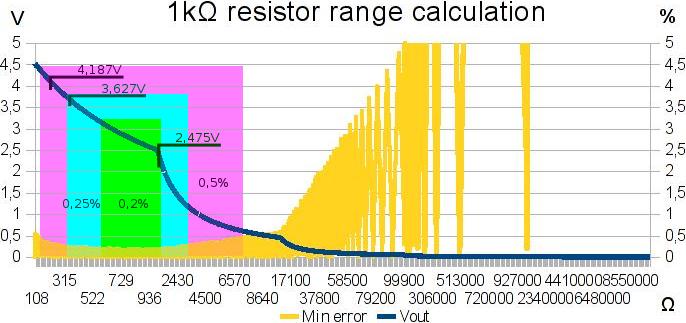
Maximal errors in reading/calculating when using combination of these resistors in 200 to 10 Mohm range for 12bit ADC is 0.102% and for 10bit ADC 0.4064%.
After simulating with new setup and 12bit ADC I got these results:
Max resolution colon is used to set up maximal resolution for 12bit ADC.
Real resolution colon contains simulated values of actual resolution.
As can be seen in error colon, errors from simulated/measured/calculated values do not go to maximal error of 0.102% and this is because combination of resistors from lover range actually adds better resolution in higher range.
To be precisely they add about 50% better resolution, which is seen as about 50% better readout.
For comparison I calculate/simulate resolution and errors for 10 bit ADC.
This shows that is possible to make decent measurement with it too, but price difference is so small and this is measure equipment after all.
Conclusion
With this setup I got far better results in simulation for measuring resistance.
There is slightly higher resolution and lower errors than in original setup.
Capacitance and inductance didn’t change much, only slightly at edges of measuring range.
Basically when using this detailed resistor ladder accurate measuring reactance can be done with only two frequencies.
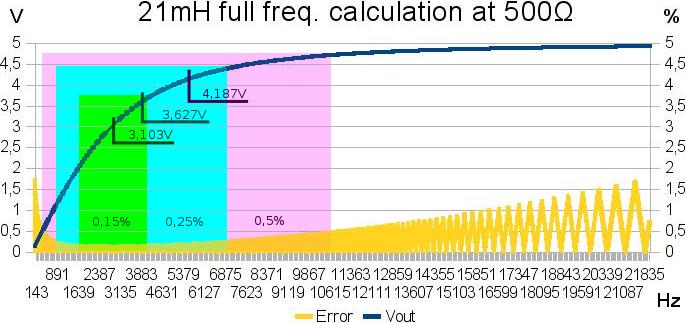
In main measurement range there is frequency around 1.1 kHz for capacitors and 2.3 kHz for inductance – frequency are for targeted point of half input voltage.
Higher frequencies are needed only for measure lower ranges; for inductors less than 30mH to increase reactance and in capacitors less than 15pF for decrease reactance.
Lower frequency is needed for higher values; more of 700H in inductance to decrease and above 1uF for increase reactance in capacitor.
This also adds to justification of usage 16 resistors for digital potentiometer, especially if experimental PC version shows that square wave AC is far worst for measure than sine.
PWM module can generate almost sine wave in this small frequency range.
4. Power supply from battery – in this case parallel PC port
With all above I practically have finish setup for analog part of my PC/LCR tweezers device.
As I mention already I plan to use 3.3V power supply.
Source in PC version would be 5V from LPT port output pins, and in tweezers from dual NiMH 2.4V/300mA batteries (4.8V).
For stable 3.3V regulator I plan to use S-1132B33 LDO Regulator with shutdown pin.
For PC version I also need voltage level translator to enable normal communication between 5V LPT port and 3.3V MCU.
1. SMD probe
For my tweezers I need some SMD probes.
At first I was planning to buy one, but pricing are too high for my taste.
So I search for alternatives on net and I find this:

- http://www.maxim-ic.com/app-notes/index.mvp/id/4459
- http://makerdude.com/blog/diy-smd-tweezers/
- http://poeth.com/SMD.htm
Therefore I plan to use only wire in middle and GND all around.
2. Protection from charged capacitors
Almost all measurement tools for capacitors have warning not to connect charged capacitor.
My LCR tweezers have the same problem, so to solve it I decide to place something between probes to shorten them.
Then if I grab charged capacitor with probes, it will be discharged.
To perform measurement I plan using switch to signal device for breaking short point and begin measurement.
With that, tweezers will be protected from discharging current and consume less power, because it will do measuring only when button is pressed.
Big problem is what to use. Obviously choice will be relay, however they are all big.
Smaller ones are reed relays but they can sustain only small currents.
Another problem with relays is that they consume a loot of power during operation.
Using MOSFET is better solution however for this I need at least 10V for gate.
That means adding voltage doublers or more. Another problem is that this protection doesn’t work when device is powered off.
So on end I decide to use switch for shortening/breaking probes and signaling device to begin measurement.
3. Digitally selected wide range of resistors
Now, what I really need is not simple 6 point selector for predefined 6 resistors like in standard DMMs.
Main problem for accurate testing resistors in voltage divider setup is to get proper resistor pair for targeted output voltage.
In measuring capacitance and inductance this isn’t that significant because I can change frequency and match reactance to used resistor.
Ideal digital potentiometer for my need would be one with range from 0 to 10Mohm in resolution of 1 ohm.
Simply put, to achieve this I’ll need 10 million combinations and this can be done with 24 bit – at least 24 resistors + switches to get from 0 to 16777215 ohms in 1 ohm resolution.
This solution of 24 bits is too big and using single chip digital potentiometers have other problems.
Biggest digital potentiometer what I found have 1Mhom (AD5241BRZ1M) in 8bit increment.
That means increment of about 3.9 kohms. But I’ll need 10 of them in series to get 10Mohms.
Fine tuning to increment of 0.39ohms can be done by putting another two of 10kohm and 100 ohm in series, however big issue is frequency bandwidth which is limited to 6 kHz.
So for my purpose digital potentiometers are not good enough.
3.1. Digital selector (shift register, microprocessor?)
So I have to do it with switches and resistors.
When it comes to selecting it is big question how to do it.
Shift register is my first choice but having lot resistors to select means calculations for them how to select it.
Now my microcontroller for this purpose must already calculate guessed value for resistor, then find/calculate closest one available from list which contains calibrated values for each resistor and then set it up.
These calculations require a loot of memory, especially for storing calibrated values.
Another microcontroller can be handy, with extra memory designated to serve only for resistors.
I find out that price between shift registers and microcontrollers are almost identical, so I chose to go with another microcontroller as replacement for shift register.
There are some other advantages in using microcontroller; mainly entire device becomes modular with two separated programming.
Another one is that main microcontroller no longer stores detailed data for each resistor and don’t have to calculate for them.
Basically my idea is; when it calculate guessed resistor, it will send that value to second microcontroller.
That one would find/calculate closest resistance for measure and return that value + set up resistors to that value.
For numerous reasons which I wouldn’t discuss here I decide to go with Microchip PICs microcontrollers.
For my needs I require 16 pins for selecting resistors thru switches (see 3.3. for number) + 3 for SPI serial communication between main microcontroller/PC and this one.
This is total of 19 pins, so suitable PIC with at least 19 I/O and Serial Communication module are PIC16F1516 and PIC24F16KA102 series.
I deicide to go with PIC24 series and main reason is speed – faster calculations, even this series is double the price of PIC16 series.
3.2. Analog switchers or Reed relays?
Now about switches; the best would be to use reed relays but this can take up much of space and most important one: consume significant amount of current in operation.
So I discard them as solution.
Analog switches are worst solution especially if used in series, but there are now available better switches than old CD4066.
I find that FSA2267 with 0.35 ohm on resistance and 45 MHz bandwidth is far better solution.
So I chose to use this switches instead.
3.3. Chosen set of resistors for optimal resistor range
This was tough one and I spend a loot of time on this.
First there was problem of deciding what setup to use; resistors in series or parallel configuration.
There are advantages and disadvantages to both.
Parallel combination provides easier calibration and reduction in errors by division - to some degree.
A problem with this is non linear result due division and calculations for selected resistor must be performed in floating point math, which is problematic with microcontroller.
When using resistors in series like ladder, analog switches are adding up their resistance resulting bigger error and problematic calibration.
On other hand result is linear and easy to calculate/set.
So even I decide at first to go with parallel combination, low resolution vs. number of resistors at higher resistance range was too great to be satisfactory.
At end I decide to go with series setup.
Obviously 24 resistors are too much and 6 are minimum.
Usually minimal set of resistors to cover entire range would be 200, 800, 9k, 90k, 900M and 9M ohms – 6 bits to cover.
Now the question is why using these exponential values?
What is optimal resolution and accuracy?
To answer these questions, I make this graph:

Here is shown difference between two values at different ADC readout points.
10 bit ADC can distinguish about 4.89mV.
So in ideal environment using 1k for testing another 1k resistor, ADC readout will be 2.5024437928V or 2.4975562072V.
After calculation we get 1001.9569471624 or 998.046875 ohms.
In both results, difference or error from real value is 0.1953125%.
As can be seen on graph, this small error is only at mid point.
Going to any edge (bigger resistor difference) produces larger error.
Note that this error is identical for any voltage. So targeting half of input voltage will get the best possible result.
To reduce this error, 12bit ADC will be better solution, which I plan to use.
My soundcard have already 16bit ADC so designing for 12bit ADC will be better solution.
To get best resolution and accuracy is to have only ADC error.
In 10 bit ADC resolution for 100 ohm is 0.1953125 ohm, for 1 kohm 1.953125 ohm up to 10 Mohm and 19531.25 ohm resolution.
Using 10 kohm resolutions at 10 Mohm measuring range is waste, because it doesn’t affect reading at ADC.
However at 12 bit ADC this would have big difference, because minimal resolution for 10 Mohm is 4882.8125 ohms.
So from this math by rounding values of 12 bit ADC, I got these resolutions:
| Resistor range | resolution | x100 | x1000 |
| 1-10 | 0.0005 | 0.05 | 0.5 |
| 10-100 | 0.005 | 0.5 | 5 |
| 100-1k | 0.05 | 5 | 50 |
| 1k-10k | 0.5 | 50 | 500 |
| 10k-100k | 5 | 500 | 5k |
| 100k-1M | 50 | 5k | 50k |
| 1M-10M | 500 | 50k | 500k |
Starting from here including possible errors and number of switches I decide to start with resolution of 1 ohm.
In range from 200 ohms to 10 kohms in resolution of 1 ohm, resistor in series must be: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096 and 8192 ohms.
This is 14 bits or 14 switches with these resistors to make that range and it’s obviously already too much.
If best resolution is multiplied by 100, errors in reading will increase by 0.000061% and will not cross 0.2% error of 10 bit ADC, which is acceptable.
For this, new resistor series in range 200 to 1 kohm would be: 10, 20, 40, 80, 160, 320 and 640 ohms with resolution of 10 ohms.
For 1k to 10k range 50 ohm resolution is needed and we use previous resistors to continue into this series: 800, 1600, 3200 and 6400 ohms.
So far 10 bits and to complete series to 10 Mohms another 12 bits are needed which is in total too much.
If resolution was increased by 1000 times, this will increase error by 0.00406% and become 0.101688021% well below 0.2% error.
Series for this resolution will be: 100, 200, 400, 800, 1k, 2k, 4k, 8k, 10k, 20k, 40k, 80k, 100k, 200k, 400k, 800k, 1M, 2M, 4M and 8M ohms.
Total of 20 bits, but this series can be optimized further, if lower resistances are combined together they form enough value to eliminate next bigger resistor.
100+200+400+800=1500 ohms which covers 1k range and with resolution in 1k-10k range of 500 ohms this fits perfectly next in line to 2k. So 1k resistor can be eliminated.
Optimization method will also eliminate others too; 10k, 100k and 1M ohm.
Now, this form series of 16 bits/switches and this is first case below 20bits which I find acceptable.
Maximal errors in reading/calculating when using combination of these resistors in 200 to 10 Mohm range for 12bit ADC is 0.102% and for 10bit ADC 0.4064%.
After simulating with new setup and 12bit ADC I got these results:
| Resistor range | Max resolution | Real resolution | Error | 10bit ADC rez. | 10bit ADC error |
| 0.1-0.2Ω | 0.0005 | 0.02437 | 19.895% | 0.09569 | 95.695% |
| 0.2-1Ω | 0.0005 | 0.02459 | 11.113% | 0.09841 | 33.324% |
| 1-10Ω | 0.0005 | 0.0271 | 2.427% | 0.1076 | 9.129% |
| 10-100Ω | 0.005 | 0.05827 | 0.263% | 0.21923 | 1.057% |
| 100Ω-1kΩ | 0.05 | 0.53292 | 0.053% | 1.94687 | 0.217% |
| 1kΩ-10kΩ | 0.5 | 5.32926 | 0.049% | 19.46875 | 0.196% |
| 10kΩ-100kΩ | 5 | 53.46679 | 0.049% | 194.6875 | 0.196% |
| 100kΩ-1MΩ | 50 | 534.9121 | 0.049% | 1946.875 | 0.196% |
| 1MΩ-10MΩ | 500 | 5351.9785 | 0.049% | 19468.75 | 0.196% |
| 10MΩ-30MΩ | 5000 | 15815.69602 | 0.053% | 63995.71428 | 0.213% |
| 30MΩ-100MΩ | 5000 | 103962.0253 | 0.104% | 413097.82607 | 0.416% |
Real resolution colon contains simulated values of actual resolution.
As can be seen in error colon, errors from simulated/measured/calculated values do not go to maximal error of 0.102% and this is because combination of resistors from lover range actually adds better resolution in higher range.
To be precisely they add about 50% better resolution, which is seen as about 50% better readout.
For comparison I calculate/simulate resolution and errors for 10 bit ADC.
This shows that is possible to make decent measurement with it too, but price difference is so small and this is measure equipment after all.
Conclusion
With this setup I got far better results in simulation for measuring resistance.
There is slightly higher resolution and lower errors than in original setup.
Capacitance and inductance didn’t change much, only slightly at edges of measuring range.
Basically when using this detailed resistor ladder accurate measuring reactance can be done with only two frequencies.
In main measurement range there is frequency around 1.1 kHz for capacitors and 2.3 kHz for inductance – frequency are for targeted point of half input voltage.
Higher frequencies are needed only for measure lower ranges; for inductors less than 30mH to increase reactance and in capacitors less than 15pF for decrease reactance.
Lower frequency is needed for higher values; more of 700H in inductance to decrease and above 1uF for increase reactance in capacitor.
This also adds to justification of usage 16 resistors for digital potentiometer, especially if experimental PC version shows that square wave AC is far worst for measure than sine.
PWM module can generate almost sine wave in this small frequency range.
4. Power supply from battery – in this case parallel PC port
With all above I practically have finish setup for analog part of my PC/LCR tweezers device.
As I mention already I plan to use 3.3V power supply.
Source in PC version would be 5V from LPT port output pins, and in tweezers from dual NiMH 2.4V/300mA batteries (4.8V).
For stable 3.3V regulator I plan to use S-1132B33 LDO Regulator with shutdown pin.
For PC version I also need voltage level translator to enable normal communication between 5V LPT port and 3.3V MCU.